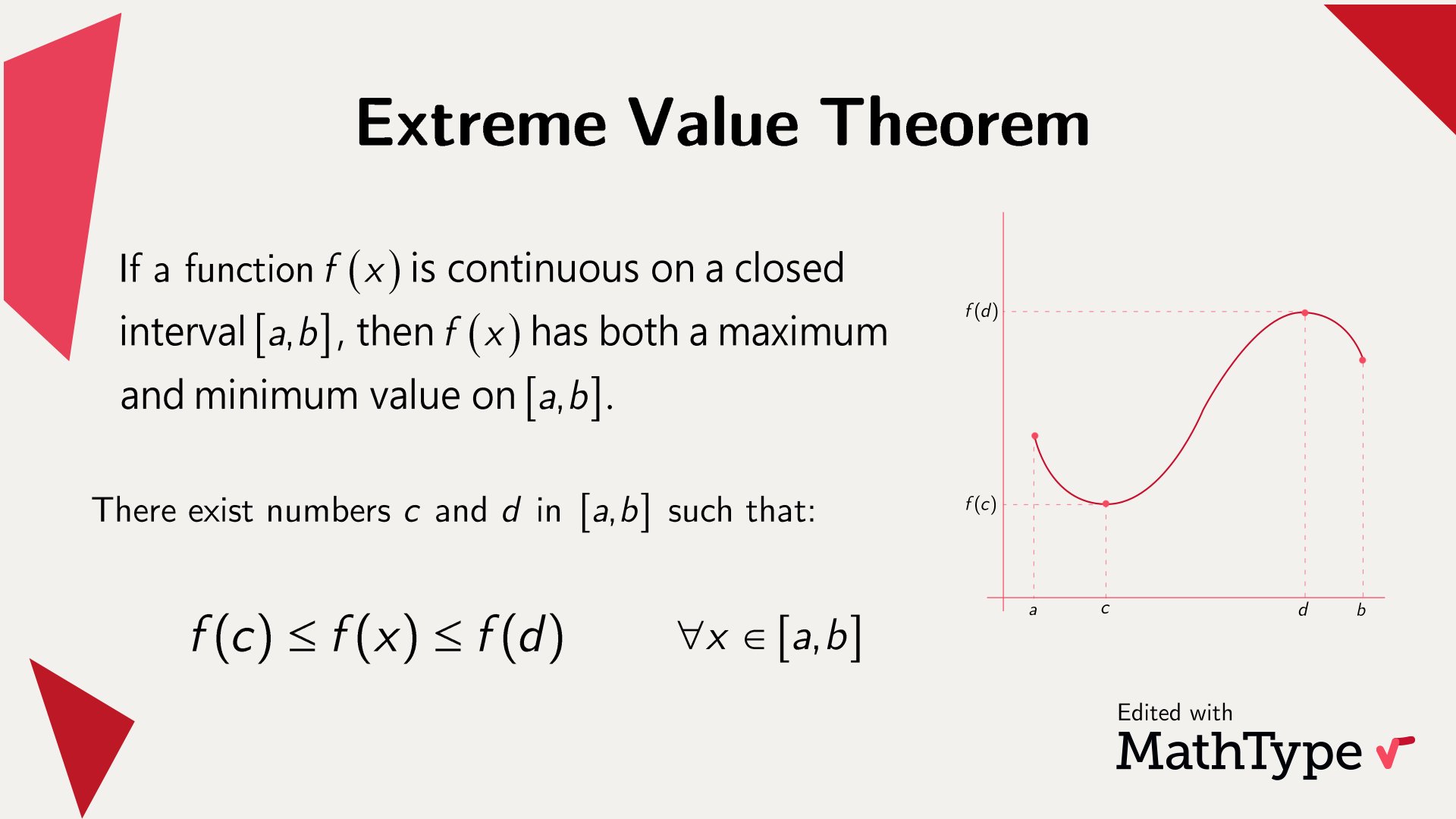
Extreme value theorem, EVT
유계된 함수에는 반드시 최댓값과 최솟값이 존재한다는 정리이다.
f:\\mathbb R \\to \\mathbb R가 구간 [a, b]에서 연속이면, \\exists M, m\\in[a,b] \\ s.t. \\ f(M) = \\max\\{f(x)\\}, \\ f(m) = \\min\\{f(x)\\}이다.
먼저 f(x)가 유계임을 증명한 후 최댓값과 최솟값이 존재함을 보인다.
2.1. f(x)의 유계를 증명 ✎ ⊖
먼저 집합 하나를 생각해보자.
\\mathbb S = \\{x\\in[a, b]|f \\rm \\ is \\ bounded \\ in [a, x])\\}
함수
f는
x=a에서 연속이므로 유계이다. 따라서
a\\in\\mathbb S이다.
a가
\\mathbb S의 원소이기 때문에,
\\mathbb S는 공집합이 될 수 없고, 그러므로
\\Bbb{S}의 최소상계
c이 존재한다.
c = \\sup \\mathbb S라 하자. 여기서
\\mathbb S\\subset [a, b]이므로
c\\leq b이다.
만약
c < b라면
f는
x=c에서 연속이고,
f가
[c-\\delta, c+\\delta]에서 유계인
\\delta가 존재한다.
c+\\delta도
\\mathbb S의 원소이기 때문에
c = \\sup \\mathbb S에 모순이다. 따라서
c=b.
모든
\\epsilon> 0에 대하여
f가
[a, b-\\epsilon] \\subseteq[a, b)에서 유계이고,
(1) [b-\\epsilon, b]에서 유계이기 때문에
(2) f는
[a, b]에서 유계이다.
2.2. 최댓값의 존재를 증명 ✎ ⊖
\\mathbb T = \\{f(x)|x\\in[a, b]\\}는 위 증명에 의해 유계이고, 상한
M=\\sup \\mathbb T이 존재한다.
다음 함수를 생각해보자.
g(x) = \\displaystyle\\frac 1 {M-f(x)}
함수
g(x)는
M=f(x)인 경우를 제외하면 유계이므로
\\not\\exists c \\ s.t.\\ f(c)=M이라 하자.
g(x)는
[a, b]에서 연속이므로
\\forall\\epsilon>0 \\ \\exists x_1 \\in[a,b]\\ s.t.\\ M-\\epsilon<f(x_1)<M \\equiv 0<M-f(x_1)<\\epsilon이다.
따라서
g(x_1)는
\\displaystyle\\frac 1 {M-f(x_1)} > \\displaystyle\\frac 1 \\epsilon 이고,
\\epsilon\\to 0^+이면
g(x_1)은 발산하며,
\\not\\exists c \\ s.t.\\ f(c)=M라는 가정이 모순임을 알 수 있다. 따라서
\\exists c \\ s.t.\\ f(c)=M이다.
2.3. 최솟값의 존재를 증명 ✎ ⊖
\\mathbb T의 하한
M=\\inf \\mathbb T이 존재한다.
다음 함수를 생각해보자.
h(x) = \\displaystyle\\frac 1 {f(x)-m}
함수
h(x)는
m=f(x)인 경우를 제외하면 유계이므로
\\not\\exists d \\ s.t.\\ f(d)=m이라 하자.
h(x)는
[a, b]에서 연속이므로
\\forall \\epsilon >0 \\ \\exists x_2 \\in[a, b] \\ s.t. \\ m<f(x_2)<m+\\epsilon \\equiv 0<f(x_2)<\\epsilon이다.
따라서
h(x_2)는
\\displaystyle\\frac 1 {f(x_2)-m} > \\displaystyle\\frac 1 \\epsilon이고,
\\epsilon\\to 0^+이면
h(x_2)은 발산하며,
\\not\\exists d \\ s.t.\\ f(d)=m라는 가정이 모순임을 알 수 있다. 따라서
\\exists d \\ s.t.\\ f(d)=m이다.


